Common Distributions
Normal Distribution
The normal distribution is an important family of continuous probability distributions. Its importance as a model in statistical procedures is due to the central limit theorem. The normal distribution may be defined by two parameters, location (mean) and scale (variance), which makes it a natural choice for a distribution. Most statistical tests work with or assume normality. The normal distribution is first introduced by French mathematician Abraham DeMoivre in 1733 and made famous in 1809 by German mathematician K.F. Gauss in his study of astronomy. As a result, it is also known as the Gaussian distribution. During mid to late nineteenth century, many statisticians believed that it was “normal” for most well-behaved data to follow this curve. A normal distribution has the following characteristics:
- A normal distribution can be completely described by knowing only the mean and variance
- Mean = Median = Mode
- Bell-shaped probability density curve
- Area under the probability density curve is the cumulative probability
- The standard normal distribution is the normal distribution with a mean of zero and a variance of one
- Transform into standard normal distribution using Boxcox transformation
Example
The life span of light bulbs is normally distributed with a mean equal to 600 hours and a standard deviation of 40 hours. Find the probability that a bulb will burn out:
- before 578 hours
- after 634 hours
- after 634 hours
The distribution of the life span of light bulbs is shown in the following figure. The probability that a light bulb will burn out before 578 hours is the area under the curve before 578. To obtain the probability value, simply transform the distribution to a standard normal distribution and get the probability values from the statistical tables.
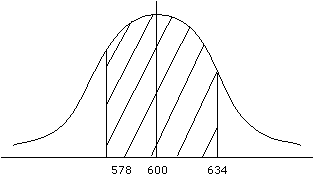
Z = (578 – 600)/40 = -0.55
P(x < 578) = P(Z < -0.55) = 0.291
Z = (634 – 600)/40 = 0.85
P(x > 634) = P(Z > 0.85) = 0.802
P(578 < x < 634) = P(-0.55 < Z < 0.85) = P(Z < 0.85) - P(Z < -0.55) = 0.5111
Binomial Distribution
The Binomial distribution is useful for attribute data in a binary nature (e.g. pass/fail, yes/no, accept/reject, etc). Data are generated usually from counting of the defectives.
The probability mass function is: 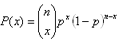 , x = 0, 1, 2, …, n
, x = 0, 1, 2, …, n
Example
If a process typically yields 2% reject rate (p = 0.02), what is the chance of finding 0, 1, 2 or 3 defectives within a sample of 100 units (n = 100)?
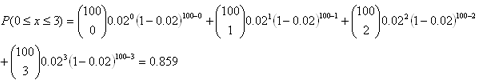
Poisson Distribution
The Poisson distribution is useful for discrete data involving error rate, defect rate (i.e. counting defects).
The probability mass function is: 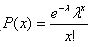 , x = 0, 1, 2, …
, x = 0, 1, 2, …
Example
If a process typically yields 4.0 defects per unit, what is the chance of finding 0, 1, 2 or 3 defects per unit?
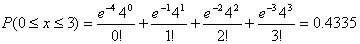
Student’s t Distribution
The Student's t-distribution (or t-distribution), is a probability distribution that is used in place of a normal distribution when the sample size is small and population standard deviation is unknown and has to be estimated from the data.