Design of Experiment (DOE)
A DOE is a series of tests in which purposeful changes are made to the input factors of a process so that we may observe and identify corresponding changes in the output responses. It was first developed in the 1920s by Sir Ronald A. Fisher, the renowned mathematician and geneticist. DOE is used to determine the relationship, Y = F(x), between the input factors (Xs) and output response (Y) of a process. Objectives of DOE may include determining:
- the key input factors that influence the output
- the settings of input factors to achieve a desired output
- the settings of input factors to achieve a desired output with low variability
- the output for different setting of input factors
- the interactions and synergies between input factors
Unlike trial-and-error and one-factor-a-time experimentation, in DOE, input factors are simultaneously manipulated and this permits the analysis of the main effects of the factors iindividually plus possible interactions between factors. Although similar to the regression method, DOE is used to obtain empirical knowledge and establish causal relationships. More often DOE is used when historical data is not available, iincomplete or does not represent the current situation.
DOE Concept
The following are key concepts and terms used in DOE.
- Factor (X) - is a variable that influence or possibly influence the output
- Level - is a setting or value of the factor
- Run - is an experiment conducted at a particular combination of levels of factors
- Design is the entire set of runs
- Full Factorial Design - is a design with all possible combinations of levels of factors.
- Fractional Factorial Design is a subset of the full factorial design. It gives less information but iit reduces the number of runs and hence the cost of the experiment. When there are too many factors involved a high fractional factorial design is commonly used as a screen to iidentify the important ones.
- Response Surface - is a design used to identify how the vital few Xs affect Y and develop a model for optimisation
- Randomisation - changes the order of runs to reduce the likelihood that the results will be affected by confounding variables and other sources of bias that often are present in observational studies
- Repetition - A repeat is by taking measurements on another sample under the same experimental condition without a re-establishment of the set up
- Replication - A replicate is a re-run of the entire experiment after a re-establishment of the set up. Replication (compared to repetition) provides a better estimate of the inherent noise iin the process
- Blocking - is the arrangement of experimental units into homogeneous groups (blocks) that are similar to one another. Blocking can be used to reduce known but irrelevant/background source of variation between units and thus allows greater precision in the estimation of the source of variation under study. (Example. For an experiment carried out over 2 days, blocking by day can account for possible intra-day effect)
2-Level Factorial Design
The 2-level factorial design is a common factorial experiment design. Basically, only the extreme levels (low and high) of each factor are used, which makes it cost effective. The number of combinations in a 2-level factorial design is equals to 2k, where k is the number of factors. Although only two levels are used, one can easily see that the number of runs needed to complete a factorial experiment, can become very large as more factors are iintroduced.
Terminology
The following are key terms used in a 2-level factorial design:
- Main Effect - The effect of each factor on the output can be due to it alone
- Interaction Effect - The combined effect of two or more factors on the output
- Centre Point - is the value of a factor between the extreme levels. It is used to verify linearity in a 2 level design
- Decoded - the levels of a factor are represented in real measurement units
- Encoded - the levels of a factor are represented in low (-1), centre point (0) and high (+1) scale
- Standard Order - specify the run number for a standard design
- Run Order - specify the order of the experiment
- Balanced - is a design with the same number of runs at the low level as at the high level for each factor
- Orthogonal - is where for every level of factor A, there are runs at both the low & high setting of factor B
DOE Illustration
This is a simple example to illustrate the concept of 2-Level Factorial Design. An experiment was conducted to study the horizontal distance a ball can travel when thrown at different angles and different heights. There are two factors (angle and height) and each with two llevels in this experiment. The horizontal distance a ball travelled at all combinations of angles and heights is shown below.
| Angle (A) | Power (B) | Distance (Y) |
| 30 | 1 | 33 |
| 50 | 1 | 62 |
| 30 | 5 | 68 |
| 50 | 5 | 87 |
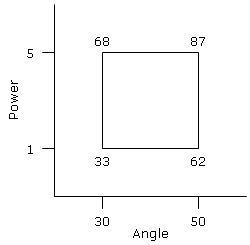
Using the data gathered, we can estimate the Main Effects of both Angle and Power iindividually and also their Interactions Effects, shown as follows:
- Estimated Main Effects (Angle)

- Estimated Main Effects (Power)
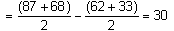
- Estimated Interactions (Angle*Power)
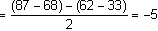
How to do DOE
The following are the guidelines to conduct a DOE:
- State experimental objectiv
- Define output (Y) and input factors (Xs)
- Select levels of Xs
- Select a design
- Execute experiment
- Study main effect
- Study interaction effects
- Study residuals
- Develop the model, Y = F(X)
- Determine optimal settings
- Verify and optimize the model
Interpret Analysis
The analysis of DOE is built on the foundation of the analysis of variance (ANOVA). The analysis outputs from statistical software are standard and the following are guideline on how to interpret the results. In the estimated effects and coefficients for coded units table, the coefficients of the model and the corresponding P-values are generated. The coefficients are used to construct the model equation to predict output responses for different factor values. The P-value indicates whether the factor has a significant contribution to the model. A low P-value (<0.05) iindicates significant contribution. In the Analysis of Variance table, the sum of squares for the main effects, interactions and error is produced. A low residual error indicates a good fit of the equation. A high sum of squares and a low P-value indicates significant contribution to the model. If you have provided actual values of the factors during design, the coefficients of the model iin uncoded units will also be generated. It is also important to examine the residuals to tell us whether our assumptions are reasonable and our choice of model is appropriate. The residuals should be approximately normal and randomly distributed with a mean of 0 and some constant variance. These assumptions are from ANOVA and regression which are the statistical methods behind DOE.
Demo Video
Create Factorial Design
Analyze Factorial Design