Capability Analysis
Capability analysis is about determining how well a process meets a set of specification limits, based on a sample of data taken from a process. It can be used to establish baseline for the process and measure the future state performance of the process for comparison.
Specification limits
Specification limits are quantified performance standards determined by customer requirements or sometimes referred to as Critical to quality (CTQ). There are two types of specification limits:
- Upper Specification Limit (USL) – specifies the maximum permissible value for the output, above which it is considered as defects.
- Lower Specification Limit (LSL) – specifies the minimum permissible value for the output, below which it is considered as defects.
The CTQ can have either one or both specification limits. For instance, the CTQ for mail delivery is speed and it may only have the upper specification limits. There is no lower specification limit because customers want the mail delivered as soon as possible. In the case of a manufactured part of a machine, its dimensions will have strict upper and lower specification limits because if the steel nut is made too big or too small, the parts may not fit iin properly.
Capability Analysis for Discrete Data
A. Defects Per Million Opportunities (DPMO)
The DPMO is one of the more common measure used to measure performance. It indicates the amount of defects in a process per one million opportunities. In Six Sigma, the goal is to reduce process output variation to within three standard deviations from the target level and this equates to more than 3.4 defects per million opportunities.

Another common measure is the Defects Per Unit (DPU) and it indicates the number of iindividual defects (or errors) on each unit. However, the DPMO is often used instead of the DPU because DPMO allow for comparison between processes with different levels of complexity. A complex process is accounted for in the DPMO calculation with a greater number of opportunities for error.
B: Terminology
The challenge in using DPMO or DPU is determining exactly what qualifies as a defect or an opportunity. DPMO can be easily inflated by having a loose definition for opportunity and a strict definition for defects. A general rule of thumb for defining an opportunity is that it should have a reasonable probability of failure and the failure should be something that is of concern to the customer. Defects can be anything that have little impact on the end product or could result in re-work or scrap but it definition should be consistent and clearly documented.- Unit: The item produced or processed. It is the specific product or service used to evaluate whether or not customer requirements are met.
- Defect: Any event that does not meet the specifications of a CTQ.
- Defective: Any unit that contains one or more defects. Such a unit is called a “defective unit”.
- Opportunity: Any event which can be measured that provides a chance of not meeting a customer requirement.
C: Sigma Performance
Given DPMO, the sigma performance, Z can be obtained from the Z-table. Divide DPMO by 1,000,000 to obtain the probability of defect, P(d). The Z-value from the table corresponding to P(d) is the sigma performance.
Capability Analysis for Continuous Data
To help us understand capability analysis for continuous data, we can look at it from a statistical perspective. The following figure shows typical frequency plots for a process output. The process outputs that are beyond the specification limits are defects and the shaded areas represent the probability of defects.
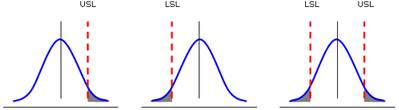
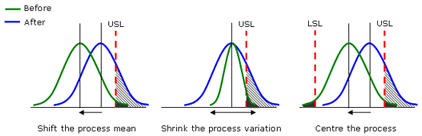
The goal of process improvement is therefore to minimize the size of the shaded area. For a process output with a one-sided specification, we can try to shift the process mean and/or shrink the variation. For an output with two-sided specifications, we also need to center the process.
Capability Indices
Cp, Process Capability
- Measures how consistent is the process relative to the specification limits.
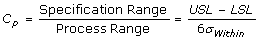
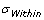
- 6 standard deviations is used because, at that range, it covers almost the entire (99%) population
- Sometimes referred to as “short term performance”, “best case performance”.
- Process needs to be in control, otherwise the calculation (of sigma) is not valid.
Cpk, Process Capability Index
- Measures how consistent is the process relative to the specification limits and also within the target specification.
- Adjustment of Cp for the effect of non-centered distribution.
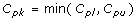
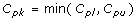
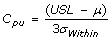 and
and 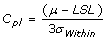
Pp, Process Performance
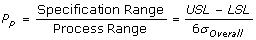
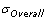 is the sample standard deviation. It represents the variability of the process within a period of time.
is the sample standard deviation. It represents the variability of the process within a period of time.- Sometimes referred to as “long term performance”.
Ppk, Process Performance Index
- Adjustment of Pp for the effect of non-centered distribution.
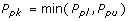
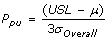 and
and 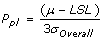
Z, Process capability measure
- Z is the number of standard deviations between the mean and the specification limit
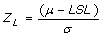
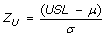
- For two-sided specification,
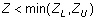 . Overall Z can be determined from the Z-tables by using the
overall probability of defects, P(d) which is the sum of probability of defects for lower specification,
P(d)L and probability of defects for upper specification, P(d)U
. Overall Z can be determined from the Z-tables by using the
overall probability of defects, P(d) which is the sum of probability of defects for lower specification,
P(d)L and probability of defects for upper specification, P(d)U
Comparing Cp and Cpk
Cp is a measurement that considers the spread of the data relative to the specification limits. As shown in the following figure, a high Cp value indicates low process variation.
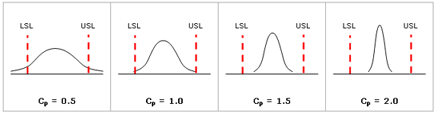
Cpk is a measurement that considers both the spread of the data and the shift of the data relative to the specification. As shown in the following figure, a process may have good Cp but not meeting specifications (low Cpk).
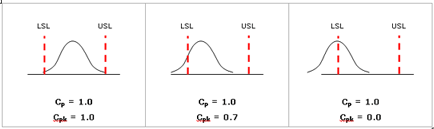
Comparing Cp, Cpk, Pp, Ppk
If a process is on-target and stable, the four indices, Cp, Cpk, Pp, Ppk should be approximately the same. In the following situations the indices may differ:
- Process is off-target but stable: Cp > Cpk and Pp > Ppk.
- Special causes present: Cp > Pp and Cpk > Ppk.
- Certain fixed pattern in subgroup: Cp < Pp and Cpk < Ppk
Caution
These days, capability indices can be easily calculated with the help of most statistical softwares available. However, it is important to note that capability indices are only useful when the process is stable. In addition, like all other statistical procedures, capability indices are only estimates based on the samples collected. Thus, control charts are often used in conjunction to monitor the process over time rather than relying on a single number.